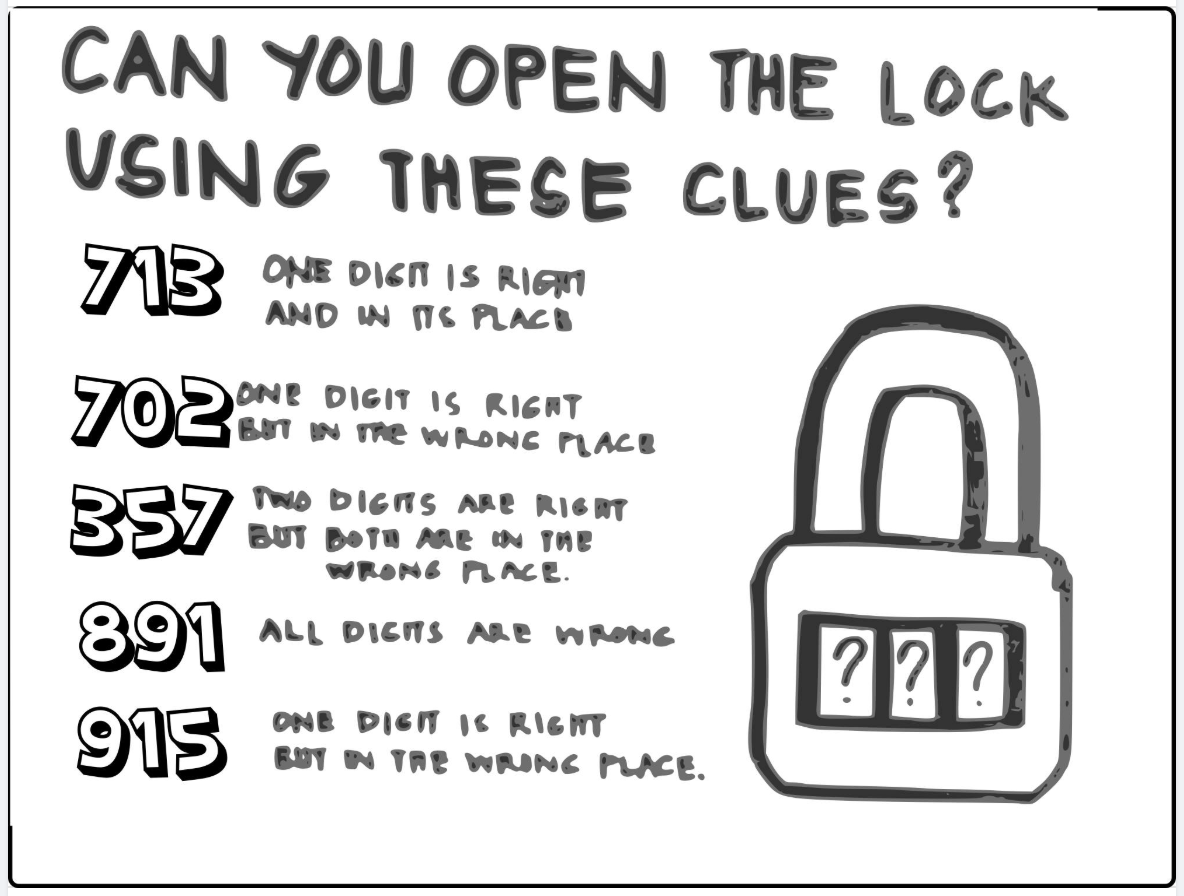
Mastermind

A friend recently posted this puzzle that I thought was pretty awesome:

This is one of those brain teasers that I think looks somewhat daunting at first, but if you have played the game Mastermind before, it’s pretty straightforward to solve.

I’ve been giving Mastermind as a software engineering programming interview exercise for more than a decade. What I like about it is that it’s easy to describe to someone who has never played the game before, and also that it has three parts to it which get progressively more difficult. This first starts off with a simple recursive algorithm (or you can solve it with binary math for those inclined) for generating a search space. It then requires you to write a slightly tricky “scoring” function for determining which digits are in the correct or incorrect places. If you’ve made it this far and there’s time left, the third part is about writing an algorithm for “solving” the code.

Here’s the code I used to solve this particular puzzle:

import itertools
  
combos = itertools.product(range(0, 10), repeat=3)
 
def score(guess, secret):
    red = 0
    g_nums = [0] * 10
    s_nums = [0] * 10

    for x in range(0, len(guess)):
        if guess[x] == secret[x]:
            red += 1
        else:
            g_nums[guess[x]] += 1
            s_nums[secret[x]] += 1
 
    white = sum([min(g_nums[x], s_nums[x]) for x in range(0, len(g_nums))])
    return red, white

def filter(guess, g_score):
    global combos
    n_combos = []
    for c in combos:
        if score(c, guess) == g_score:
            n_combos.append(c)

    combos = n_combos

def main():
    filter((7, 1, 3), (1, 0))
    filter((7, 0, 2), (0, 1))
    filter((3, 5, 7), (0, 2))
    filter((8, 9, 1), (0, 0))
    filter((9, 1, 5), (0, 1))

    print combos

if __name__ == "__main__":
    main()

Let’s start off with the first part, which is generating the search space. Here I’m being extremely lazy. There are 10³ (i.e. 1,000) potential “combinations” to choose from to find the correct “combination” to open the lock. This is where I hate the word “combinations” because it’s not really technically correct. A combination implies that order of the digits doesn’t really matter, but in this case, that’s not true. It’s also not technically correct to say that there are 1,000 “permutations” for our “combination” because a permutation implies that we can’t use the same value more than once (i.e. there are not 10!/7! or 720 permutations). In this case, we’re using a permutation with repetition, or more specifically the cartesian product of the three sets of 10 digits. What ‘itertools.product()’ is doing is creating a generator with 1,000 tuples which look like: (0, 0, 0), (0, 0, 1), (0, 0, 2), … (9, 9, 7), (9, 9, 8), (9, 9, 9).

For the interview I give, I usually use colours instead of digits (at least for the examples), and I use 8 possible colours, and 4 positions instead of 3. Using powers of two makes the math a lot tighter for software engineers since we’re used to working that way. Typically the candidate also writes a recursive function here to solve this, although often things go off the rails here either because recursion can be tricky, or because they try to write it iteratively and don’t want to use four nested for loops. Key to doing well here is really understanding how many times the inner part of your for loop is being called. Also, I don’t mind if candidates use things like itertools() because it just shows that they understand how to use a language, so if they want to write a one liner, that’s just perfectly fine.

After generating the search space, the scoring function comes next. The scoring function takes two codes and compares them against each other to determine two things: How many digits are in the right place, and how many are correct but in the wrong place. In the game this is given by “red” and “white” markers respectively, hence why I chose those as variable names in the code. The biggest thing to remember is that there is an order of operations where we need to get the “red” values before we get the “white” values. What I mean by this is that we should check for the right colour/digit being in the right place before we check to see if it’s the write colour/digit in the wrong place.

For any values which are not in the correct place, we’re going to create a tally for both the guess and the secret number. Let’s say we had two numbers, (5, 2, 1) and (1, 1, 3). We would put (5, 2, 1) into the tally array so that it would look like:

[0, 1, 1, 0, 0, 1, 0, 0, 0, 0]

That is, we have one 1, one 2, and one 5. If we take (1, 1, 3), it would look like:

[0, 2, 0, 1, 0, 0, 0, 0, 0, 0]

We have two 1’s, and one 3.

To get the number of numbers which were in the incorrect place, we can compare the tallys for each number and take the sum of the minimum values. Most of the time we’re just comparing 0’s, so we don’t increase the total sum, but for the number 1, we have two 1’s in the guess, and one 1 in the secret, so min(2, 1) gives us 1, which is the total of correct numbers in the incorrect place.

The third and final part of the code is writing the filter function. For this we take the search space we already generated (the 1,000 tuples), and we iterate through each of them comparing them against the number we’re guessing and then checking to see if the result of the scoring function matches our guess score. The cool thing about the scoring function is you can feed numbers in either way and they will always give us the same score. For our example we could give (5, 2, 1) and (1, 1, 3) for either the guess or the secret or switch them around and we would always get back the same score. For each of the two numbers that we’re going to check (our guess number and each number in our search space), we only keep ones which match our guess score.

This technique actually throws out a lot of numbers really quickly. If you look at the size of the search space each time we run it against a filter, we get the correct answer after just three guesses. That’s because the score gives us a lot of information about what we’re looking for, even if we guessed something that was entirely incorrect.